This Appendix discusses some of the following key steps in designing a
monitoring programme:
- Defining the objective;
- Gaining an understanding of variability;
- Defining the target population;
- Choosing the precision and confidence;
- Determining the number of samples;
- Determining when and how often to sample.
A2. Defining the objectives
The importance of clearly defined, quantitative objectives to the
design and implementation of sound, cost-effective sampling programmes cannot be
overstated. Without careful consideration of the aims of the sampling, the data produced
may well be inappropriate, and the number of values generated be either too small or
unnecessarily great - with obvious cost penalties in either case. The definition of the
objectives has been fully discussed in Section 3.
Previous sections in the report have discussed the questions of (a)
what determinants to measure, and (b) how to measure them. For simplicity, therefore, the
following discussion is in terms of a discrete sampling programme for one particular
chemical contaminant of interest. The same basic principles discussed below apply,
however, to all other types of sampling, chemical or biological.
A3. Gaining an understanding of variability
Statistical sampling is primarily concerned with estimating some
underlying property of interest (a mean or a 95%ile, perhaps) in an environment of
uncertainty. If there were no variability, there would be no need for sampling. Sources of
variability involved in measuring the real world can usually be separated into two very
distinct types. These are
- Systematic variability (i.e. due to physical/temporal processes such as seasonality,
diurnal cycle, tidal height, long-term trend, etc.), and
- Random variability (i.e. unpredictable or unexplainable fluctuations).
Variability introduced by the analytical process can fall into either
of the above categories. With no extra information about what is being sampled other than
the sample values themselves, all the variability appears to be random. However, by adding
knowledge, sources of systematic variability can be identified and therefore the random
component can be reduced.
The greater the random component of variability, the more samples will
be needed to obtain a worthwhile result. That is no more than common sense. The impact of
systematic variability, however, is less obvious. A particular systematic cycle that is
not taken account of by the sampling programme design can have an effect indistinguishable
from random error - and so weaken the effectiveness of the sampling programme. But where
knowledge of that systematic cycle is exploited by the programme design - either by
sampling at a fixed point in the cycle, or by arranging for the sampling to 'average out'
the cyclic effect - the programme can actually be made more effective.
The soundest way of exploring these issues is by conducting a
statistical analysis of historical data relating to the water body under investigation
(assuming such data are available). This is a valuable preliminary for three main reasons:
- it provides a measure of the variability (measured by the standard deviation, 's') that
is needed for sample-size calculations;
- it helps to identify systematic components, and hence - by allowing 's' to be reduced -
improve the efficiency of the sampling programme; and
- it allows an appropriate statistical model to be determined for describing the random
variability. (Normal? Log-normal? Some other distribution? Unrecognisable?)
A4. Defining the scope of the sampling programme
The scope of the sampling programme is simply the temporal and spatial
bounds within which the monitoring will take place, i.e. the sampling population. Ideally
this scope would be defined to be the 'target population'. The target population is the
collection of all parts of European water resources, temporal and spatial, about which
inferences need to be made in order to meet the objectives of the monitoring network. This
may be as much as all of Europe's water resources, or it could be a certain part of it
defined by the nature of the objectives. For instance, if the objectives require the
calculation of the winter mean concentration then the target population would be all water
resources sampled during the winter months.
In many situations, however, the scope of the sampling programme will be restricted to
a subset of the target population due to practicalities of sampling and costs. This is
acceptable if inferences drawn from the sampling population can be reliably extrapolated
to the target population. If the sampling population is not an adequate substitute for the
target then it is necessary to resolve, or at the very least acknowledge, the conflict
between an ideal but impracticable target population, and a convenient but inappropriate
sampling scope.
One way of doing this is to change the wording of the objectives so that they take
account of the restriction on the target population, enabling future users to judge for
themselves the risks involved in extrapolating the results of the sampling programme to
other circumstances.
The following examples illustrate the resolution of the scope of the sampling
programme.
- Example 1
Objective:
To monitor an effluent discharge to check its compliance with an annual
95th percentile concentration limit.
Target population:
All possible equal-sized aliquots that can be drawn from the effluent
at very small intervals of time apart (i.e. samples can be taken from any part of the
effluent and at any time).
Sampling population:
Could be the same as the target population if there was an automatic
sampler (which could be activated at any time of the day or night, any day of the week)
drawing from the sole point of discharge.
If sampling was done manually, the sampling population might have to
exclude time outside of normal work shifts (night-time, bank holidays, etc.). This
restricted scope would be sufficient if there was no systematic difference between daytime
and night-time concentrations, say.
Alternatively, or in addition, the scope of the sampling programme
would be a restricted subset of the target population if there were several discharge
points, but sampling could only be done at one of them. The sampling population would be
adequate if there were no differences between effluent quality from point to point.
- Example 2
Objective:
To estimate the difference between annual mean concentrations of a
particular pollutant in a receiving water upstream and downstream of the discharge.
Target population:
There are two parts to the target population. the first is all possible
equal-sized volumes of water that can be drawn from the receiving body at very small
intervals of time apart, from any depth and any site in the water providing that it is
upstream of the discharge and does not contain any part of the effluent. The second is the
same as the first with the exception that the possible sampling sites must be downstream
of the discharge and not influenced by other discharges or sources of pollutant.
Sampling population:
In addition to the possibility of temporal restrictions such as those
outlined in the first example, the scope of the sampling may be limited by other factors.
For instance, it may not be possible to establish whether or not a particular upstream
sampling site is free of the effluent being monitored as it may depend on stream flow
rates and mixing patterns etc. In such a situation, the upstream sampling population might
be restricted to sites more than a certain distance upstream of the discharge but
downstream of any other sources of pollutant. Results from this sampling population are
very likely to be reliably extrapolated to the target population.
A5. Compliance testing/threshold excedence
Most European compliance testing is of the 'exceeding the threshold'
variety, i.e. no more than 'x' excesses out of 'n' tested samples. In this case if
information is reported as 'pass' or 'fail' against a level or standard then common
numbers of samples are needed for fair comparisons.
A6. Percentile estimation and estimation of averages
If all the data used in calculating each statistic, or just the
statistic and some estimate of variance (e.g. standard deviation), are provided then it is
possible to judge the quality of the estimates and determine how significantly different
they are from each other. Having a common sampling frequency for a determinant would not
ensure the estimates produced in different areas would have the same quality, or even a
minimum quality, because of the differences in variability from area to area.
A better approach would be to specify a minimum level of precision and
confidence to which the estimates must conform (i.e. a minimum estimate of quality). The
minimum number of samples required to achieve this precision and confidence can then be
calculated for each site or area. The following sub-section defines what is meant by
precision and confidence and the sub-section after that describes how this can be used to
determine the minimum number of samples.
A6.1 Precision and confidence
The reason for designing a sampling programme in the first place is because it is not
possible to sample the whole of the target population. Therefore, the values obtained for
the statistical objectives are estimated from a (usually) much smaller sub-population of
samples and are, consequently, subject to a certain amount of error or uncertainty.
Choosing the precision and confidence sets limits on how much of this uncertainty can be
tolerated in the results of the programme.
Consider some quantity that has been estimated from the sampled data. This estimate
will almost always differ from the true value (i.e. the quantity which would be calculated
if the whole of the target population was sampled). Answering the following two questions
will define the precision and confidence.
- What is the largest discrepancy that can be tolerated between the answer given by the
sampling programme and the true value? This is the desired precision.
- What degree of confidence should there be that the answer obtained does in fact lie
within the desired precision? This is the desired confidence.
Confidence is expressed as a percentage, so for example, a confidence
of 99% means that if the sampling programme could be repeated 100 times, the answer would
be within the precision tolerance on 99 occasions.
A6.2 Determining the number of samples
Once the precision and confidence have been set and some estimate of
the random variability of the samples is known (based on previous monitoring results),
then the minimum sampling frequency can be derived.
By way of a simple example, suppose that the intention is to estimate
the mean of some determinant over a year. The standard formula for calculating the
required number of samples (assuming that the random variability of the samples can be
modelled by a Normal distribution) is:
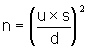
where
n is the minimum number of samples needed,
d is the desired precision,
u is a factor related to the desired confidence (obtained from the
percentiles of the standard Normal distribution), and,
s is a reliable estimate of the variability (expressed as the
standard deviation).
[If the desired confidence is C%, then the factor u is
the (100+C)/2th percentile of the standard Normal distribution. For example, if C
is 95 then u is 1.96 (the 97.5th percentile).]
\tab \tab
Table A.1 below shows the effects of different confidences and
precisions on the numbers of samples needed. The table combines the desired precision and
the random variability by using the relative precision (the ratio of precision to standard
deviation).
Table A.1 Minimum numbers of samples needed to obtain certain
precisions and confidences.
|
Confidence, C |
Relative precision, d/s |
90%
(u = 1.65) |
95%
(u = 1.96) |
99%
(u = 2.58) |
99.9%
(u = 3.29) |
0.1 |
273 |
385 |
666 |
1083 |
0.2 |
68 |
96 |
167 |
271 |
0.3 |
31 |
43 |
74 |
121 |
0.4 |
17 |
24 |
42 |
68 |
0.5 |
11 |
16 |
27 |
44 |
0.6 |
8 |
11 |
19 |
30 |
0.8 |
5 |
6 |
11 |
17 |
1.0 |
3 |
4 |
7 |
11 |

This example relates to the simplest statistical
objective, i.e. estimating a mean. However, the same principle applies to more complicated
statistical objectives (e.g. the median, 10th percentile geometric mean, etc.).
A7. Potential impact on current monitoring practice
To gain some understanding of the levels of sampling ideally required
for an EEA network some estimate of variance is required for each determinant. These can
best be drawn from current monitoring practices. To take the example of river nutrients a
key determinant is soluble reactive phosphorus (SRP). The National Rivers Authority of
England and Wales has an extensive network of sites which will monitor for SRP in its
proposed general quality assessment scheme (GQA). To obtain an average estimate of
variance all means and standard deviations were calculated for all of the 5,000 sites
sampled more than 12 times over the three years between 1990-1992.
As riverine orthophosphate levels follow a highly skewed distribution
(approximately log-normal) the values of the site standard deviations are spread across a
large range (4 orders of magnitude). A log transformation of the sample values before
calculating the standard deviations reduces the spread of these standard deviations to one
order of magnitude. The advantage of this technique is that the spread of precisions
obtained for each site will be correspondingly small allowing a better overall assessment
of the number of samples required. The average estimate of standard deviation for the loge
transformed data was calculated to be 0.74. This estimate of variability can now be
applied to assess the number of samples required to meet a particular precision.
The classification used in the Dobrí\'9a Assessment (1995) has six
classes with boundaries for orthophosphate at 25, 50, 125, 250 and 500 \'b5g/l of PO4-P.
The lowest of these classes represents a site with no anthropogenic input and the highest
class indicates a site with high levels of nutrient input either through agricultural
run-off or sewage input. We can specify the desired precision and confidence in terms of
the width of the classes. For example, we may wish to be 90% confident that a site
reported as class B is really class B (i.e. its true geometric mean SRP lies between 25
and 50 m g/l) when its geometric mean SRP is more than 25% of
the class width away from the class boundaries. To achieve this we need to take enough
samples at the site; the minimum number of samples required is given by the equation in
the previous section, i.e.
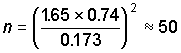
where 0.74 is the average standard deviation of loge SRP and
0.173 is the precision (one quarter of the typical class width on a log scale). This
formula can be rearranged to estimate confidence intervals associated with particular
sampling frequencies. Table A.2 below presents widths of confidence intervals based on log
transformed orthophosphate data.
Table A.2 Widths of confidence intervals based on log transformed SRP
data from the National Rivers Authority of England and Wales GQA database
Number of samples |
Mean of samples |
relative lower 90% |
relative upper 90% |
6 |
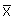
|
0.61 |
1.65 |
12 |
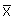
|
0.70 |
1.43 |
18 |
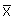
|
0.75 |
1.34 |

Note: This is to gain the required precision at each site. A different
number would be required for regional or larger scale aggregation of data.
For example, if the mean orthophosphate concentration of a site sampled
12 times was 100 \'b5g/l we could say with 90% confidence that the value lies between
70\'b5g/l and 143 \'b5g/l. This precision may well be expectable. Few monitoring programs
sample their sites at an intensity of 50 times per year. There are several options:
- choosing fewer and/or more widely separated boundaries.
- tolerating the precision and report the values with a lower confidence
- combine samples over a period greater than one year, to produce a rolling
classification, that is one year use 1990 to 1992 data, next use 1991 to 1993 data and so
on.
For inter-regional comparisons, the number of sites per region needs to
be specified having first specified the number of samples per site. If, by way of example,
we take the whole area of the National Rivers Authority of England and Wales to be one
region (or strata, see Section 6) then we can estimate the number of sites required using
the formula given in Section 6.3. The intra-region (intra-stratum) standard deviation of
site geometric means is 1.62. If we wanted a precision of one half of the class width and
a confidence of 90% for inter-regional comparisons, then the required number of sites is
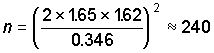
A8. Determining when and how often to sample
Having determined how many samples should be taken, the next task is to
decide on the duration of the sampling programme, and how to spread the samples over that
total sampling period. In other words, once the question 'How many?' has been answered,
the questions 'How often?' and 'When?' then need to be addressed.
A8.1 Defining the timescale
Many objectives - especially those relating to compliance assessment -
have a pre-determined duration. For other types of enquiry a period of 12 months is often
convenient (though the traditional idea of an annual statement of quality should not be
perpetuated merely by default).
Where the choice is more open, it is ultimately a matter of weighing up
the extra costs of carrying out the sampling over a shorter time period against the
benefits of obtaining the results that much sooner.
A8.2 Allocating the sample times
The main issue here is whether to allocate the samples at random, or
whether to spread them systematically (through time, or by volume, or some combination of
these, according to the identified target population). The choice depends very much upon
(a) the objective, and (b) what is known about the variability of the system. The
principal advantage of random sampling is that it is statistically foolproof - a
particular advantage when little can be assumed about the system being sampled. (It is
also an essential component of any regulatory sampling programme, incidentally, as it is
the only way of retaining the element of surprise.)
Strict random sampling does, however, pose severe organisational
difficulties Moreover, it does not guarantee that the results from any one sampling
programme will be particularly representative. For these reasons, systematic sampling will
often be a preferable alternative. With such a regime, however, it is important to be sure
that the sample times and dates do not unwittingly move in step with some important cycle
in the physical system - unless, of course, it is intended to exclude this from the target
population. For example:
- Sampling only at 12:00 every Monday will give no information on either a diurnal or a
weekly cycle.
- Sampling at 12:00 every eighth day would systematically cover all days of the week and
so incorporate all aspects of the weekly cycle, but still say nothing about diurnal
variation.
- Sampling every seven days and 13 hours would eventually cover both the entire 24 hour
clock and the seven-day week, and so cover the widest possible target population.
- Sampling at every high tide would also cover diurnal and weekly cycles, but would
obviously exclude any effects associated with the tidal cycle.
A9. Time-based and volume-based sampling
There are two fundamentally different ways in which we can visualise
quality variations in a river:
- the time-based description (in which concentration is plotted against cumulative time),
and
- the volume-based description (in which concentration is plotted against cumulative
flow).
If flow was constant through time the two representations would be
identical. Otherwise, the volume based description can be thought of as being a
'distorted' time-based version in which the clock is driven by a water-wheel rather than
by clockwork.
Virtually all routine water quality monitoring is time-based rather
than volume-based. For example, the sampling regime for a river will be expressed as
'sample once a fortnight' rather than 'sample once every 4000 MI'. As most of the EEA's
objectives relate to concentrations, the time-based description is the correct one to use.
When the primary interest is in, say, mean loads, there is an inherent
disadvantage with time-based sampling: a straightforward mean concentration will in
general lead to a biased estimate of load. As high flows occur for a relatively short
time, very few will happen to coincide with the sampling occasions. (There might also,
indeed, be a deliberate policy of avoiding sampling on occasions of very high flow for
safety reasons.) The resulting concentration versus flow plot will therefore have a great
preponderance of low-flow points. As a consequence, evidence for a significant association
will always hinge unsatisfactorily on at most a handful of high-flow samples. With sample
sizes of only 30 or 40, moreover, there is a real risk that high flows are entirely
under-represented. The danger then is that the sample variability badly under-estimates
the true variability in the underlying population, and so leads to unrealistically
optimistic statements of precision (Ellis, 1989).
With a volume-based approach, in contrast, sampling frequency will
automatically be stepped up in periods of relatively high flow (as, for example, with
flow-proportional sampling devices), and so the mean concentration at the end of the year
provides a direct estimate of mean load.
The report on current EEA surface water quality monitoring networks
(Kristensen and Bøgestrand 1996) identifies 19 sampling programmes which are specifically
designed to assess contaminant loads in river systems across Europe. The report indicates
that without exception these programmes all have time rather than volume driven sampling
regimes.
Calculation of loads can be addressed in two ways using an annual
average flow to produce a simple arithmetic mean of load or use the instantaneous flow
associated with each sample to produce a flow-weighted average. Both of these approaches
have their associated pitfalls when compared to flow driven sampling regimes.
Walling and Webb (1985) used a two-year sequence of hourly suspended
sediments data from a sampling station on the River Exe, together with corresponding
hourly flows provided by South West Water. Using this virtually continuous record, they
were able to mimic the results of weekly, fortnightly and monthly sampling programmes and
hence demonstrate for any particular load estimation formula (i) its average bias, and
(ii) the relationship between precision and number of samples. For the full data set there
was a positive underlying association between concentration and flow, and this resulted in
load estimates based on the simple arithmetic mean approach to underestimate the true
value. In this instance, the estimates from weekly and fortnightly programmes were on
average only 38% of the true load, whilst for the monthly programmes the ratio dropped
still further to 25%. In contrast, the flow-weighting approach showed negligible bias.
The lack of bias, though desirable, is not everything, and the
simulation results also clearly highlighted the greater imprecision necessarily introduced
by flow-weighting when there is a positive association between concentration and flow. In
other words, errors from repeated use of the flow-weighted approach will average out in
the long run, but the estimate in any one application may be a long way from the true
figure.
The Helsinki Commission which is responsible for the Convention on the
Protection of the Marine Environment of the Baltic Sea Area provides the only identified
example of a flow driven sampling program. The approach taken by the commission to produce
reliable data includes pollution load compilations (PLC's) from land-based sources. The
associated sampling strategy is aimed at providing precise estimates of input load and has
three components:
- monitored rivers
- partly monitored rivers
- non-monitored rivers.
Experience has shown the positive correlation between periods of high
river flow and high load input, especially for heavy metals, suspended solids and
nutrients. For all rivers a minimum of 12 data sets are collected throughout the year, the
data does not have to be collected at regular monthly intervals but at a frequency which
appropriately reflects the expected river pattern, measurements should, therefore, cover
low, mean and high flow data to gain a more representative assessment of contaminant load.
The benefits of flow related sampling are clear to see. These have to be carefully
weighed against the increased cost and logistical consideration of adapting this approach
to met the Agency's needs.

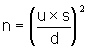
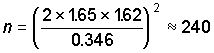
Document Actions
Share with others